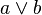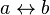Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями.
Алгебру логику называют также алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения. В булевой алгебре высказывания принято обозначать прописными латинскими буквами: A, B, X, Y. В алгебре Буля введены три основные логические операции с высказываниями? Сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений.
Логические выражения могут быть простыми и сложными.
Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В простом логическом выражении возможно только два результата — либо «истина», либо «ложь».
Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания.
Операция НЕ — логическое отрицание (инверсия)
Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:
• если исходное выражение истинно, то результат его отрицания будет ложным;
• если исходное выражение ложно, то результат его отрицания будет истинным.
Для операции отрицания НЕ приняты следующие условные обозначения:
не А, Ā, not A, ¬А.
Результат операции отрицания НЕ определяется следующей таблицей истинности:
| A | не А |
| 0 | 1 |
| 1 | 0 |
Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.
Приведем примеры отрицания.
1. Высказывание «Земля вращается вокруг Солнца» истинно. Высказывание «Земля не вращается вокруг Солнца» ложно.
2. Высказывание «Уравнение у = 4х + 3 в промежутке -2 < х < 2 не имеет корня» ложно. Высказывание «Уравнение у = 4х + 3 в промежутке -2 < х < 2 имеет корень» истинно.
3. Высказывание «4 — простое число» ложно. Высказывание «4 — не простое число» истинно.
Принцип работы переключателя настольной лампы таков: если лампа горела, переключатель выключает ее, если лампа не горела — включает ее. Такой переключатель можно счи¬тать электрическим аналогом операции отрицания.
Операция ИЛИ — логическое сложение (дизъюнкция, объединение)
Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое бу¬дет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.
Применяемые обозначения: А или В, А V В, A or B.
Результат операции ИЛИ опреде¬ляется следующей таблицей истинности:
| A | B | А или B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.
Приведем примеры логического сложения.
1. Рассмотрим высказывание «В библиотеке можно взять книгу или встретить знакомого». Это высказывание формально мож¬но представить так: С = А ˅ В, где высказывание А — «В библиотеке можно взять книгу», а В — «В библиотеке можно встретить знакомого». Объединение этих высказываний при помощи операции логического сложения означает, что события могут произойти как отдельно, так и одновременно.
2. Рассмотрим высказывание «Знания или везение — залог сдачи экзаменов». "Успешно сдать экзамен может тот, кто все знает, или тот, кому повезло (например, вытянут единственный выученный билет), или тот, кто все знает и при этом выбрал «хороший» билет.
Кто хоть однажды использовал елочную гирлянду с параллельным соединением лампочек, знает, что гирлянда будет светить до тех пор, пока цела хотя бы одна лампочка. Логическая операция ИЛИ чрезвычайно схожа с работой подобной гирлянды, ведь результат операции ложь только в одном случае — когда все аргументы ложны.
Операция И — логическое умножение (конъюнкция)
Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Применяемые обозначения: А и В, А Λ В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:
| A | B | А и B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
Приведем примеры логического умножения.
1. Рассмотрим высказывание «Умение и настойчивость приводит к достижению цели». Достижение цели возможно только при одновременной истинности двух предпосылок — умения И настойчивости.
Логическую операцию И можно сравнить с последовательным соединением лампочек в гирлянде. При наличии хотя бы одной неработающей лампочки электрическая цепь оказывается разомкнутой, то есть гирлянда не работает. Ток протекает только при одном условии — все составляющие цепи должны быть исправны.
Законы логики
Законы логики отражают наиболее важные закономерности логического мышления, В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений в соответствие с законами логики.
Закон тождества. Всякое высказывание тождественно самому себе: А = А
Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А — истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно: A & ¬A = 0
Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение истина: A v ¬A = 1
Закон двойного отрицания. Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание: ¬ ¬A = A
Кроме логических законов, важное значение для выполнения преобразований логических выражений имеют правила алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.
Законы Моргана: ¬(A v B)= ¬А & ¬В
¬(A & B)= ¬А v ¬В
Правило коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можноменять местами логические переменные при операциях логического умножения и логического сложения:
Логическое умножение Логическое сложение
A & B = B & A A v B = A v B
Правило ассоциативности. Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять:
Логическое умножение Логическое сложение
(A & B) & C = A & (B & C) (A v B) v C = A v (B v C)
Правило дистрибутивности. В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:
Дистрибутивность умножения Дистрибутивность сложения
относительно умножения относительно сложения
(a x b) + (a x c) = a x (b + c)
(A & B) v (A & C) = A & (B v C) (A v B) & (A v C) = A v (B & C)
Рассмотрим в качестве примера применения законов логики и правил алгебры логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение:
(А &. В) v (A & ¬В).
Воспользуемся правилом дистрибутивности и вынесем за скобки А:
(А & В) v (А & ¬В) = А & (В v ¬В).
По закону исключенного третьего В v ¬В = 1, следовательно:
А & (В v ¬B) = А &. 1 = А.
Таблицы истинности
Таблица истинности — это таблица, описывающая логическую функцию.
Конъюнкция
| Дизъюнкция
| Сложение по модулю 2
| |||||||||||||||||||||||||||||||||||||||||||||
Импликация
| Эквиваленция
| ||||||||||||||||||||||||||||||||||||||||||||||
Штрих Шеффера
| Стрелка Пирса
| Отрицание
|